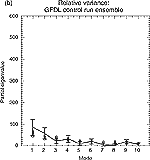
  Figure 8.17: (a) Partial eigenvalue spectrum for the EOFs from eleven CMIP AOGCMs. The observations (heavy line), together with their 95% confidence limits (vertical bars), are obtained by projecting the observed surface air temperature (Jones and Briffa, 1992; Rayner et al., 1996) onto the common EOFs obtained from eleven CMIP AOGCMs. (b) as in (a) except for ten separate 100-year segments of the GFDL control run. Taken from Barnett (1999). |
Barnett (1999) concatenated the annual mean near-surface temperature anomaly fields from the first 100 years of integration of eleven CMIP control experiments to produce common empirical orthogonal functions (EOFs) for the eleven AOGCMs. By projecting the Global Sea Ice and Sea Surface Temperature (GISST) annual mean temperature anomaly data set (Rayner et al. 1996) onto these common EOFs, he was able to estimate to what extent model variability represented the observed variability. An analysis of the partial eigenvalue spectrum for the different models (Figure 8.17a) suggests that there is considerable disparity between the estimates of variability within the coupled models. Some of this disparity arises from model drift and other low-frequency variability. Intra-model disparity was much lower than inter-model disparity as demonstrated by a similar common EOF analysis obtained from ten 100 year segments in the 1,000 year GFDL_R15_a control run (Figure 8.17b). While the highest two modes were substantially underestimated in the GFDL_R15_a model, the higher modes agreed better with observations. Error bars on the observational data are large and when this is taken into account, model disagreement with observations may not be significant. As Barnett (1999) did not remove the trend over the 20th century in the GISST data set, the observations also contain responses to both natural and anthropogenic forcing. One would therefore expect control integrations from coupled climate models to underestimate the observed spectrum at low frequencies (e.g., Folland et al., 1999).
An analogous study by Stouffer et al. (2000) compared the surface air temperature variability from three long 1,000-year CMIP integrations (GFDL_R15_a, HadCM2, ECHAM3/LSG (Large-Scale Geostrophic ocean model)) to the variability found in the same observational data set (Jones and Briffa, 1992; Jones 1994). They argued that, over the instrumental period, the simulated variability on annual to decadal time-scales was fairly realistic both in terms of the geographical distribution and the global mean values with a notable exception of the poor simulation of observed tropical Pacific variability (Figure 8.18). The HadCM2 model substantially overestimated tropical Pacific variability, whereas it was underestimated in the GFDL_R15_a and ECHAM3/LSG models. They also noticed that on the inter-decadal time-scale, the greatest variance in the models was generally located near sea-ice margins close to regions of deep oceanic convection and associated with low-frequency variations of the thermohaline circulation. While the three models generally agreed on the dominant modes of variability, there was substantial inter-model disparity in the magnitude of each mode. The analysis of Stouffer et al. (2000) can easily be reconciled with Barnett (1999) by realising that Stouffer et al. (2000) examined a subset (GFDL_R15_a, HadCM2, ECHAM3/LSG models) of those CMIP models considered by Barnett (1999) that did not experience climate drift, and that less emphasis was placed on the poor resolution of tropical Pacific variability.
As an extension to the above analysis, Bell et al. (2000) compared annual mean surface air temperature variability in sixteen CMIP control simulations to the thermometer record, on time-scales of 1 year to 40 years (Figure 8.19). The authors found that: (1) thirteen of the sixteen CMIP models underestimate variability in surface air temperatures over the global oceans; (2) twelve of the sixteen models overestimate variability over land; (3) all the models overestimate the ratio of air temperature variability over land to variability over oceans. These results likely reflect problems in both the ocean and land-surface components of climate models. In particular, underestimation of variability over oceans may be due, at least in part, to weak or absent representations of El Niño in the models; overestimation of variability over land may be due to poor land surface parametrizations including insufficient soil moisture.
Duffy et al. (2000) also partitioned the CMIP models into those that are flux adjusted and those that are not. They defined two measures of temperature variability and applied them to the CMIP control simulations. The simulations differed substantially in the amount of temperature variability they showed. However, on time-scales of 1 year to 20 years, the flux adjusted simulations did not have significantly less variability than the non-flux adjusted simulations; there is some suggestion that they may have more variability. Thus it cannot be argued, for example, that the use of flux adjusted models in studies of detection of anthropogenic climate change tends to make observed temperature changes seem more significant than they should be, compared to natural internal climate variability. Nevertheless, it is still an open question as to how coupled model variability depends on internal model parameters and resolution.
There have been relatively few studies which have undertaken a systematic comparison of AOGCM variability with variability found in the Holocene proxy temperature record. However, three studies (from the MPI (Max Planck Institute), Hadley Centre and GFDL) that focus on the analysis of long control integrations are available. Barnett et al. (1996) demonstrated that the GFDL_R15_a (Stouffer et al., 1994) and ECHAM1/LSG (Cubasch et al., 1994) models underestimate the levels of decadal-scale variability in summer palaeo-temperature proxies from 1600 to 1950 (expanded version of Bradley and Jones, 1993), with increasing disparity with observations at lower frequencies.
Using annual and decadal mean near-surface palaeo-temperature reconstructions at seventeen locations Jones et al. (1998) demonstrated, through a principal component analysis, that the standard deviation of the GFDL_R15_a model (Stouffer et al., 1994) and the HadCM2 model (Johns et al., 1997; Tett et al., 1997) principal component time-series compared favourably with both proxy and observed data. Time-series of the top seven principal components did, however, show much less century time-scale variability than in the proxy time-series. This was especially true in the HadCM2 model that was dominated by tropic-wide decadal variability. Through cross-spectral analysis they concluded that the “GFDL control integration bears a remarkable similarity in its statistical properties to that obtained from the proxy data. In view of this similarity it appears the spatial structures from the control integration can be used to represent the spatial structures of naturally occurring variations in near-surface air temperature”. This conclusion was also highlighted by Delworth and Mann (2000) who noted that both palaeo-temperature reconstructions (Mann et al., 1998) and the GFDL_R15_a coupled model suggest a distinct oscillatory mode of climate variability (with an approximate time-scale of about 70 years) of hemispheric scale and centred around the North Atlantic.
|
Other reports in this collection |
|
